Engineering Graphics is a representation of three-dimensional objects in the two-dimensional form. It generally gives detailed information about shape, size, surface, material, technology, etc. It is the graphic language from which a trained person can visualize the objects.
DRAWING INSTRUMENTS
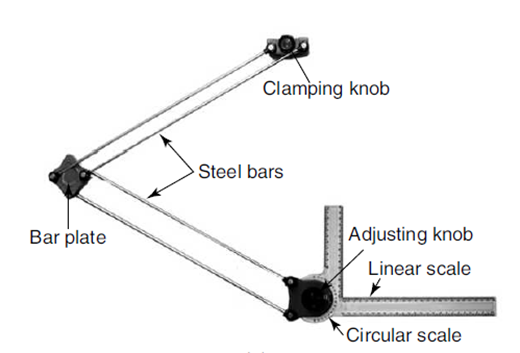
In order to master engineering drawing, it is imperative to understand the drawing instruments and how to apply them. Right choice of drawing instruments must be done with great care to ensure accuracy is achieved with ease. Below is a list of common drawing instruments and their accessories:
TITLE BLOCK:
Title box Example:
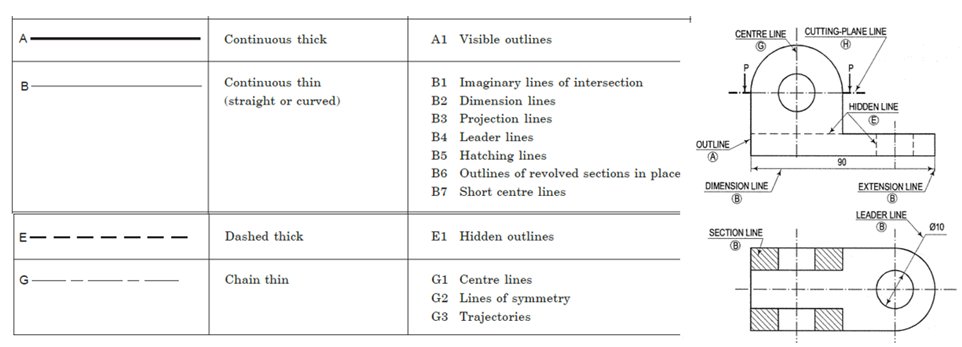
LINES:
LETTERING:
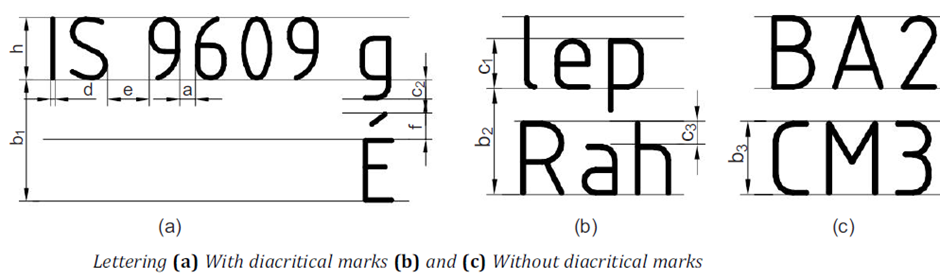
Arrow heads:
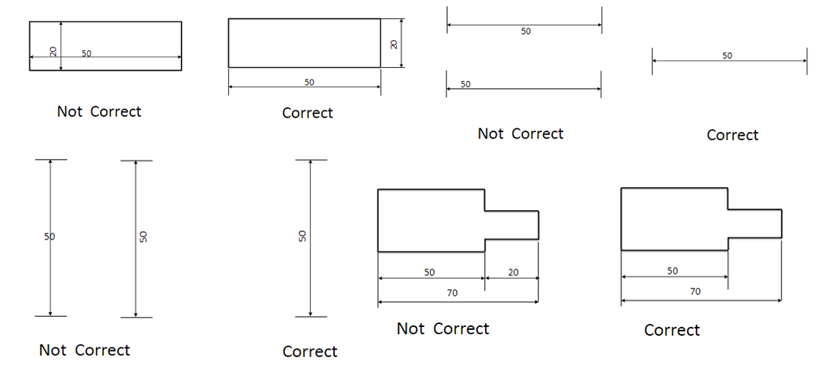
DIMENSIONING:
GEOMETRICAL CONSTRUCTIONS:
Bisect (a) an 80 mm long line and (b) a circular arc AB.
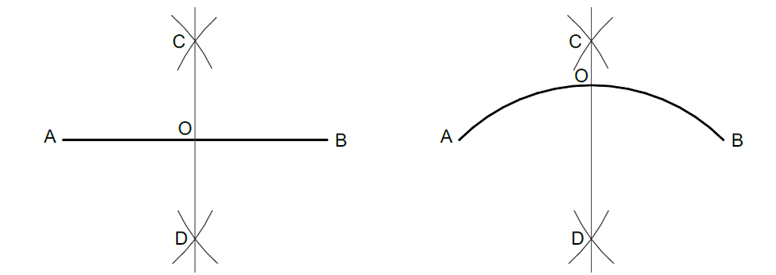
Step-by-Step Procedure:
1. Construct AB Line Segment
- Begin by marking two endpoints on the AB line segment and O which lies approximately on the mid-point of the line.
2.Compass Width Setting:
- Open the compass to slightly more than half the length of Line AB so that the arcs swept from A and B intersect.
3. Mark Arcs A-B:
- Position the compass pointer on A.
- Draw two arcs one on top and one below the line segment. The arcs halves are long enough such that the arcs marked from B meet them in the next step.
- Arcs are marked as C on the upper intersection and D on the lower intersection.
4. Arcs from Point B:
- Adjust Martin’s arcs but do not touch the two wide spans already drawn, and adjust the B. Arc marking pointed to the A.
- Draw two arcs above and below the line segment AB which cut across the arcs made from Point A.
- These intersections are expected to find points C and D which are located above and below the line respectively.
5. Finally, a perpendicular bisector is drawn:
- With the help of a ruler, stretch a straight line through points C and D.
Let us show that this line is the perpendicular bisector of line segment AB, by demonstrating that it divides AB into two equal parts and intersects it such that the intersection is at O, and the angle formed is exactly 90 degrees.
The implications of the perpendicular bisector is that it cuts AB into equal lengths and its at right angles to AB touching O.
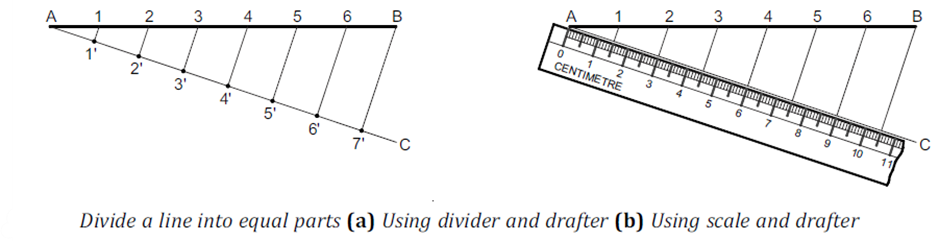
Problem: Divide an 80 mm long straight line into seven equal parts
Problem: Divide a 50 mm diameter circle into 12 equal segments.
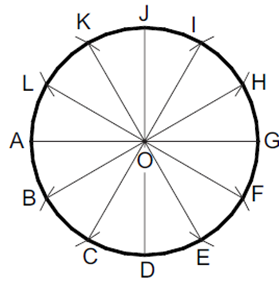
or we can divide the circle into 12 equal parts by taking 360/12. Each angle is 300.
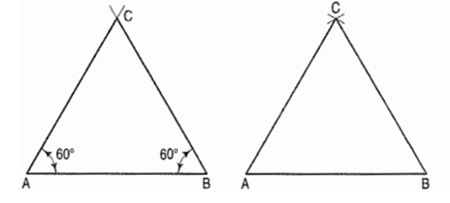
Problem: To construct Equilateral triangle
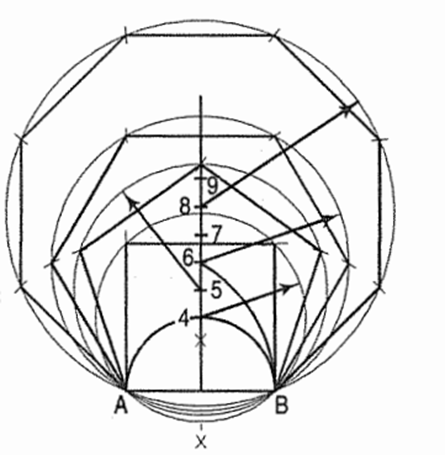
Construction of Regular Polygons (General Methods)
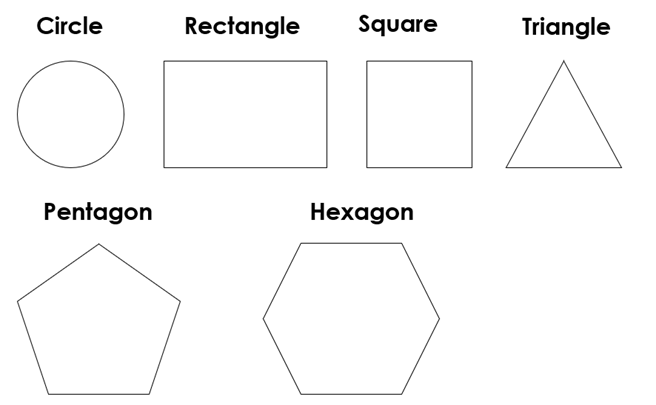
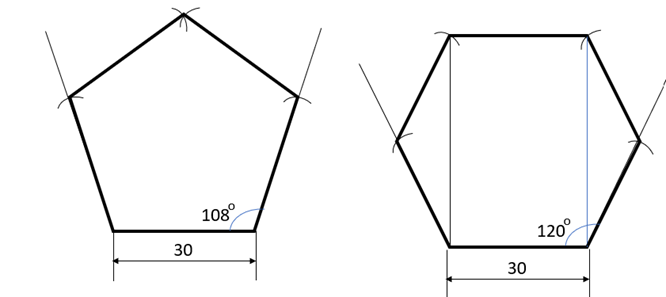
How to construct the Pentagon and Hexagon
Types of shapes
